§
The Setting
The Congestion Game is played on a network of interconnected routes or roads where individuals decide which paths to take to their destinations. These choices are driven by finding ways to navigate through the network efficiently. However, as more individuals opt for the same routes, congestion emerges, resulting in slower travel for everyone on those routes. This situation emphasizes the intricate interplay between individual decisions and their collective impact on overall traffic flow.
§
Braess's Paradox
Consider the following network. The roads from A to D and C to B are wide, so the travel time is constant no matter how many cars there are. However, the paths from A to C and D to B are narrow, so the more cars use it, the more time it takes to cross.
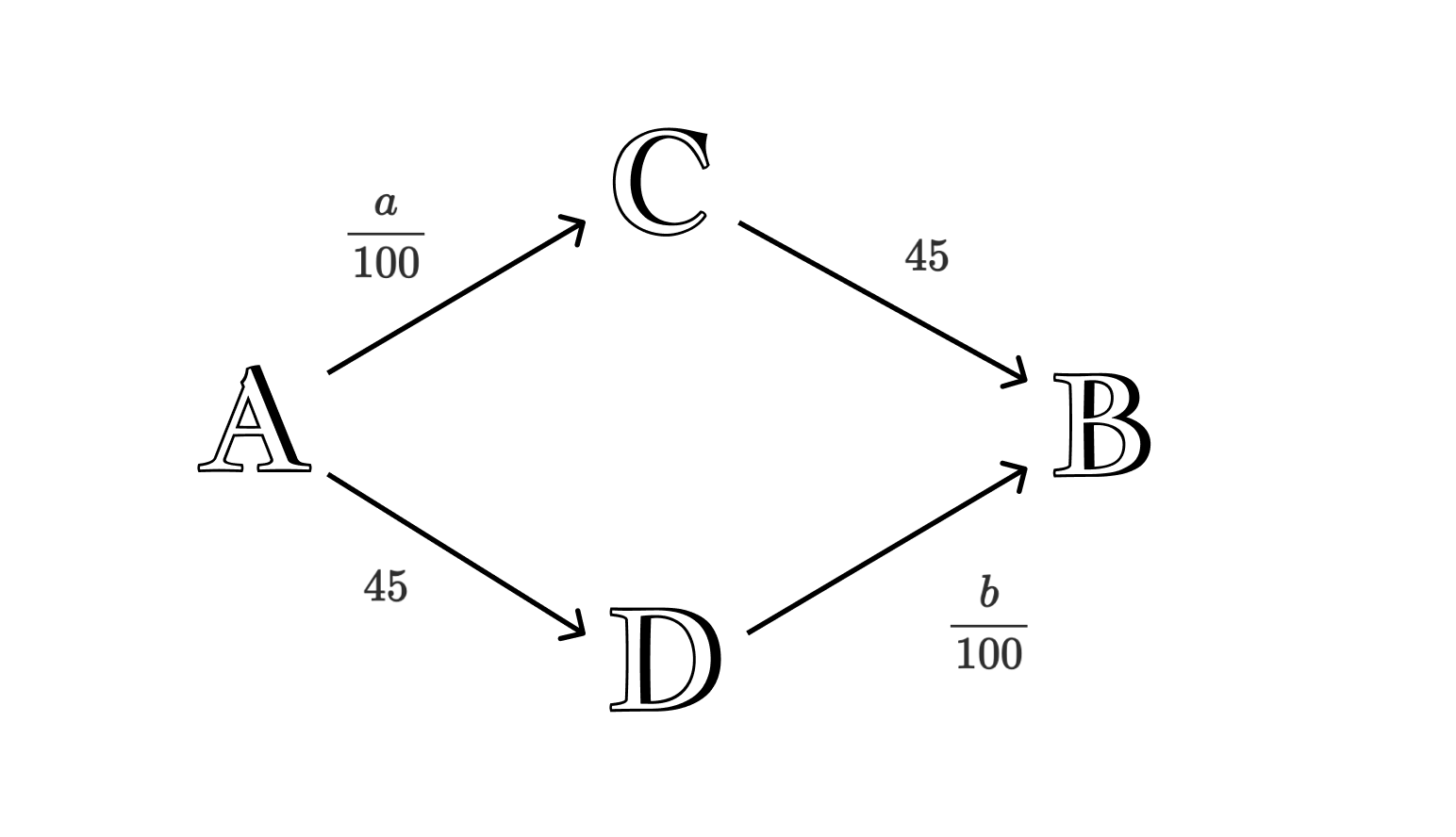
Let there be 100 drivers in this game. What is then the "Nash equilibrium"?
Nash Equilibrium
A Nash equilibrium is a situation in which each participant in a game or decision-making scenario makes the best choice they can, given the choices of others, and no one has the incentive to change their decision unilaterally. In other words, players can only improve their outcome by changing their strategy if the other players' strategies remain the same. Strictly speaking, S_i is the set of all possible strategies for player i. And s* be the so-called strategy profile, the set of all the current strategies each player uses. And let s*_-i be the set of all current strategies each player uses except for player i. Then s* is a Nash equilibrium if and only if the following statement holds
The u function calculates each player's individual "score" with the current strategy profile.
Well, it is simple, just 2000 drivers take the ACB path, and 2000 others take the ADB path. And if anyone takes the other path, their travel time will be greater. The travel time in this scenario is (2000 / 100) min + 45 min = 65 min. Now let's add a road from C to D, which will take to cross approximately 0 minutes.
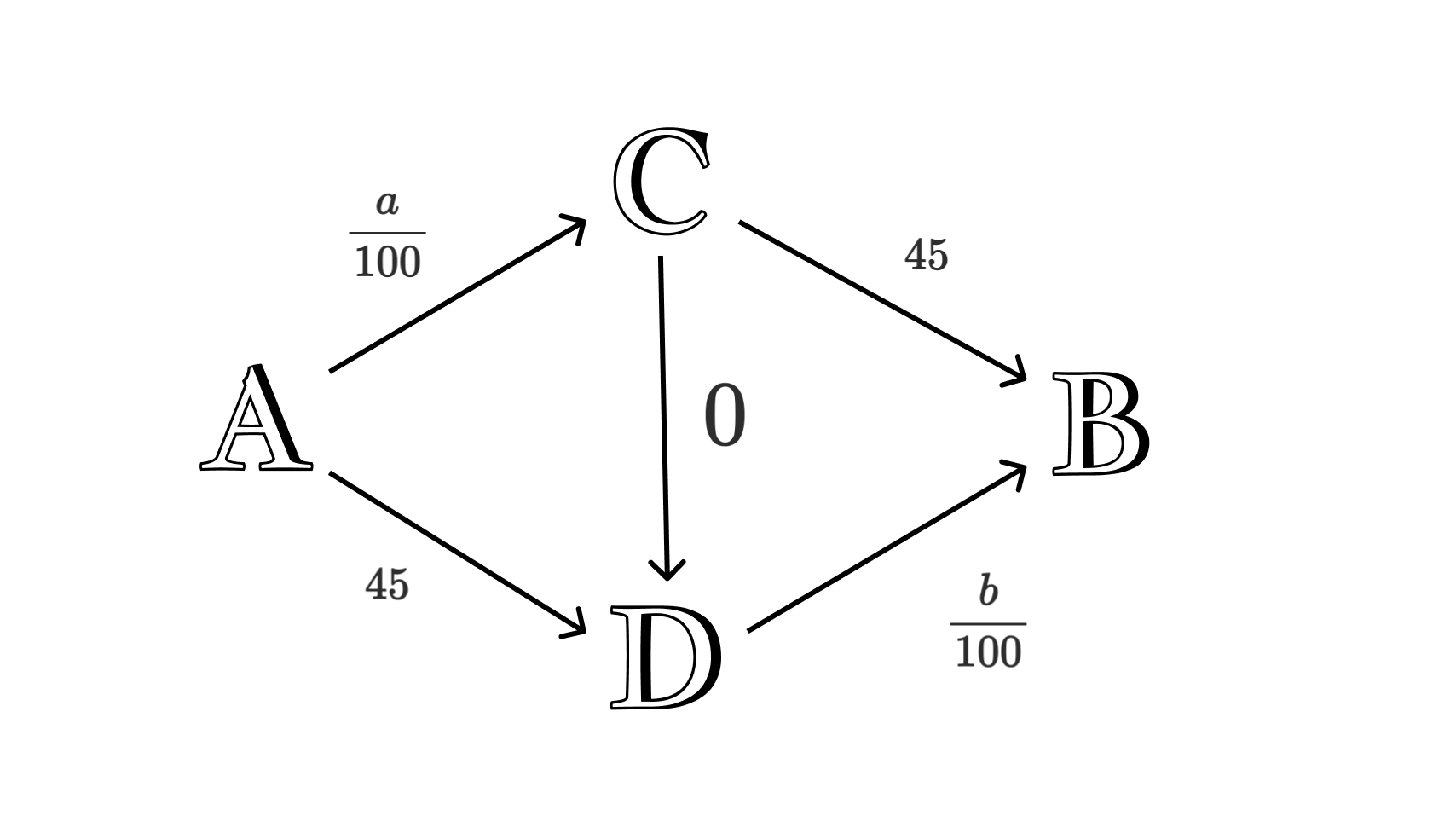
Consider the previous Nash equilibrium. Now it is no longer a valid Nash equilibrium because switching and taking the ACDB path will take him longer.
Which is better than the previous result by about 25 minutes. After trying other possibilities, you will notice the only Nash equilibrium here is if all 4000 take the path ACDB. Now let's calculate the travel time here.
If anyone switches to another path, their travel time will be greater.
So this is a Nash equilibrium. Adding a new road may sometimes lead to a greater overall travel time.
§
Playground
| Road | Travel Time, min |
|---|---|
| AD | 45 |
| AC | x |
| CB | 45 |
| CD | 0 |
| DB | x |
| Path | Drivers | Time |
|---|---|---|
| ACB | UNKNOWN | UNKNOWN |
| ADB | UNKNOWN | UNKNOWN |
| ACDB | UNKNOWN | UNKNOWN |