MrMineev

The harmonic series, is an infinite sum of the reciprocals of integers.

Does this converge? This is what I will be covering in this post.

First, we should notice the following. Replace all the denominators with the next largest power of two, then the resulting series is smaller than the original. This is simple to say, as all the denominators are now bigger or equal to the original, the values of the fractions must be less or equal than the original.

Now notice that the fraction 1/(2^n) repeats exactly 2^(n - 1). This is easily seen if you look at the previous fraction 1/(2^(n-1)). It has the last fraction of this form for the number 1/(2^(n-1)). What about the fraction 1/(2^n), well the last fraction of this form is 1/(2^n). Knowing this we conclude the number of fractions of the form 1/(2^n) must be the difference between 2^(n-1) and 2^n.

Now going back to the harmonic series, let us group all fractions that are the same. Then notice the following.

Meaning all the groups, have the same sum which is 1/2.

Notice the last expression diverges, this means the original sum the harmonic series also diverges.

We can quickly approximate the harmonic series by noticing the following.

And we know that this integral is just the natural logarithm.

So we can just approximate the harmonic series with a natural logarithm. You can make a better approximation if you also use the Euler–Mascheroni constant (this is left for the reader to look in to).

Also this approximation also proves the original statement. Because we know the following.

And we know that the natural logarithm diverges, meaning the harmonic series also diverge.

Using the fact that the harmonic series diverge, let us play a game, a stacking game.

In this game you can place a new block by pressing the "Add" button, and then you can move the block around. Now you don't want the system to fall, so you need the center of mass to not exceed the first block borders. To recalculate the center of mass line just press the "Recalculate" button. To clear everything press "Clear". Using the fact that the harmonic series diverges we can say for certain that we can extend the blocks as far to the side as we want without the system collapsing. Here is how to do this.

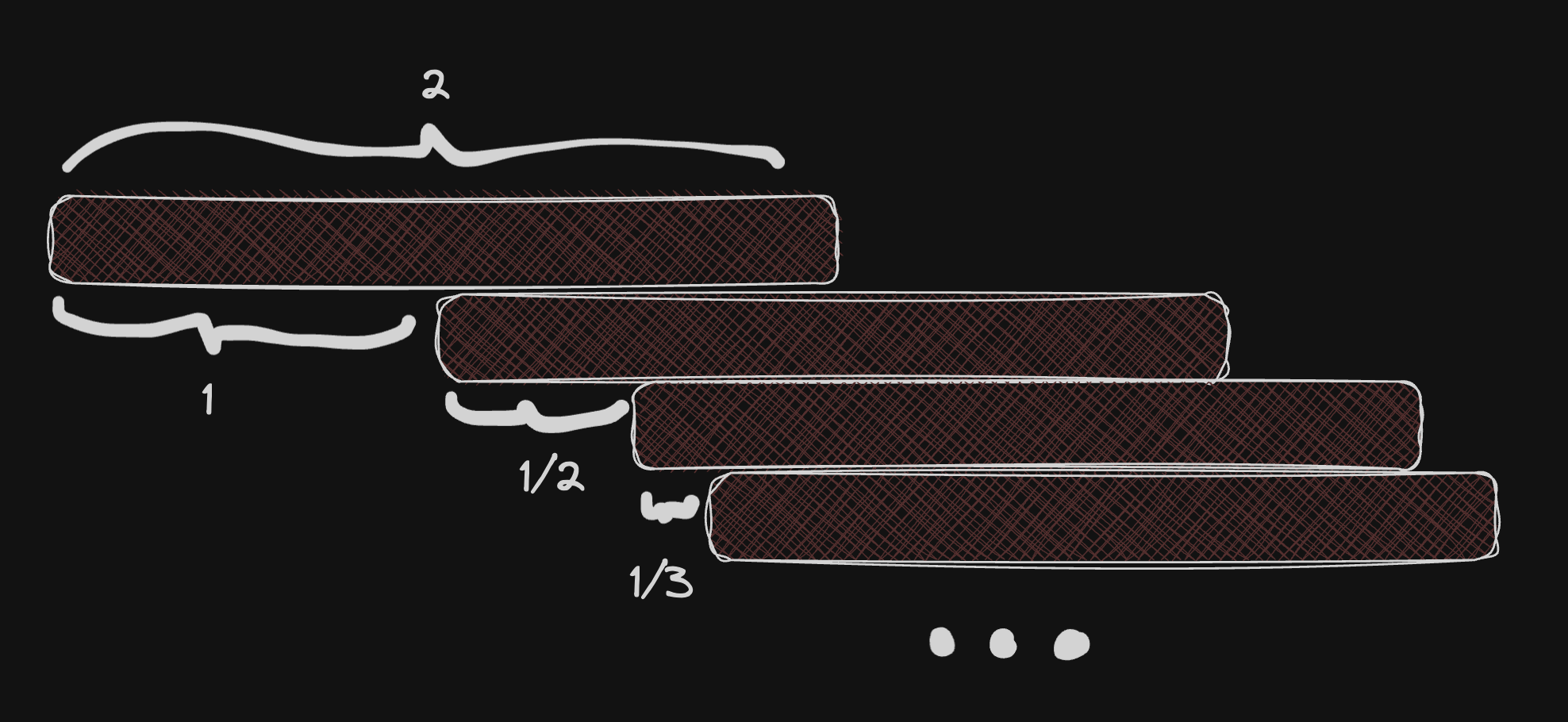
You can simply check that this construction works, this is left as an excersise.

Wikipedia   https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)

mathscareers.org.uk   https://www.mathscareers.org.uk/the-infinite-block-stacking-problem-or-the-leaning-tower-of-lire/