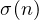 , which returns the sum of all the divisors of the
number
, which returns the sum of all the divisors of the
number 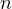 . An interesting formula that has been proven to hold is the
following.
. An interesting formula that has been proven to hold is the
following.
An important function directly related to the topic of Perfect Numbers is the Sigma
function, denoted as 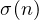 , which returns the sum of all the divisors of the
number
, which returns the sum of all the divisors of the
number 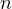 . An interesting formula that has been proven to hold is the
following.
. An interesting formula that has been proven to hold is the
following.
| (1) |
Consequently, the condition given to perfect numbers can be directly rewritten regarding the sigma function.
| (2) |
Which can be rewritten given the previous formula.
| (3) |
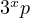 form
formThe interesting part about the formula given above is that it is now possible to
search for perfect numbers given some prime factoring. For example, consider we
want to find all perfect numbers of the form 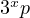 , where
, where 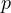 is prime. Simply
substituting this into our equation gives us quite a simple equation.
is prime. Simply
substituting this into our equation gives us quite a simple equation.
| (4) |
Simplifying everything will give the following.
2 ⋅ 3xp -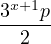 = = 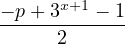 | ||
| 4 ⋅ 3xp - 3x+1p = -p + 3x+1 - 1 | ||
| 3xp = -p + 3x+1 - 1 |
In the end, we get the final equation representing this situation.
| (5) |
The right-hand side is always negative, thus for equality to hold, the left-hand
side, term 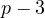 must also be negative, in other words
must also be negative, in other words 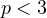 or
or 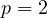 . For
. For
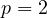 the result is
the result is 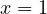 , thus the only perfect number of the form
, thus the only perfect number of the form 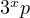 is
6.
is
6.
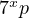 form
formAnother example to test the method on a simple yet harder prime factoring form is
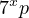 . Thus, one is required to solve the following equation.
. Thus, one is required to solve the following equation.
| (6) |
| 7x+1p - p + 7x+1 - 1 = 12 ⋅ 7xp | ||
| - p - 1 = 5 ⋅ 7xp - 7x+1 |
In conclusion, we are left with the following equation.
| (7) |
It is trivial to notice that the right-hand side is always negative, and the right-hand
side is negative only for 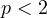 , yet there is no prime number less than two, thus is
no perfect number of the form
, yet there is no prime number less than two, thus is
no perfect number of the form 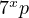 . From here, I believe it should be intuitive to
guess that the form
. From here, I believe it should be intuitive to
guess that the form 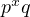 must be approachable similarly by noticing that the
right-hand side of some developed equation is negative and, from there, developing an
algorithm for finding perfect numbers of that form. That is what I am going to do in
the following section.
must be approachable similarly by noticing that the
right-hand side of some developed equation is negative and, from there, developing an
algorithm for finding perfect numbers of that form. That is what I am going to do in
the following section.
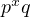 form
formAn interesting prime factoring form is 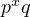 , which describes the first several perfect
numbers.
, which describes the first several perfect
numbers.
| 6 = 2 ⋅ 3 | ||
| 28 = 22 ⋅ 7 | ||
| 496 = 23 ⋅ 31 | ||
| 8128 = 26 ⋅ 127 | ||
| 33550336 = 212 ⋅ 8191 | ||
| 8589869056 = 216 ⋅ 131071 |
It seems most perfect numbers are represented in their prime factorization by two factors. Substituting this into the formula at the start gives the following.
| (8) |
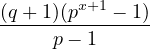 = = 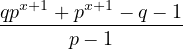 = 2pxq = 2pxq | ||
| qpx+1 + px+1 - q - 1 = 2pxq(p - 1) | ||
- q - 1 = 2pxq(p - 1) - qpx+1 - px+1 = px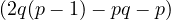 |
Thus, the general equation governing the behavior of perfect numbers of the form
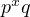 is quite simple.
is quite simple.
| (9) |
Notice that the left-hand side is always negative (this is the exact same
argument used when analyzing the previous prime factoring form). Thus, the
value 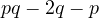 must be negative. Obviously the value is negative when
must be negative. Obviously the value is negative when
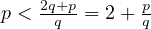 . From this, we can conclude the following interesting
relationship.
. From this, we can conclude the following interesting
relationship.
| (10) |
One would think this relationship is useful because given 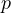 or
or 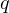 , you can limit
the search for the second variable and simply brute force all the combinations for the
second variable. However, if you take a close look at the inequality it tells us that for
big enough
, you can limit
the search for the second variable and simply brute force all the combinations for the
second variable. However, if you take a close look at the inequality it tells us that for
big enough 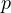 ,
, 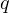 must equal 1, however 1 is not a prime number, thus there exist
no perfect numbers of such form for big enough
must equal 1, however 1 is not a prime number, thus there exist
no perfect numbers of such form for big enough 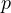 . In this case, it is simple to see
that by big enough, I mean
. In this case, it is simple to see
that by big enough, I mean 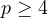 . The only two prime numbers less than four are 2
and 3. Perfect numbers of the form
. The only two prime numbers less than four are 2
and 3. Perfect numbers of the form 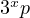 have been analyzed in the section before
this, and I have shown that the only perfect number of this form is 6. Thus,
the only perfect numbers of the form
have been analyzed in the section before
this, and I have shown that the only perfect number of this form is 6. Thus,
the only perfect numbers of the form 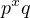 are of the form
are of the form 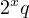 (note
an interesting property is that all perfect numbers of the form
(note
an interesting property is that all perfect numbers of the form 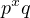 are
even).
are
even).