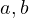 and
and  .
.
When dealing with polynomials, it is sometimes useful to introduce the idea of
Symmetric Polynomials. A Symmetric Polynomial is simply a polynomial that has
the same result no matter the order in which the input variables are given. The
simplest example would be the product of three variables 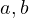 and
and  .
.
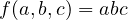
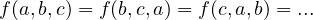 . Swapping
the values of some of the variables with each other does not change the outcome. If
one tries to generate all symmetric polynomials with three variables, which sort of
satisfy a ”simplicity” rule (which for now is not well defined), then they might end
with such a result.
. Swapping
the values of some of the variables with each other does not change the outcome. If
one tries to generate all symmetric polynomials with three variables, which sort of
satisfy a ”simplicity” rule (which for now is not well defined), then they might end
with such a result. 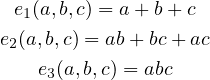
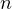 , is often denoted as
, is often denoted as 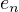 or sometimes
or sometimes 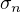 . From this definition, you can
try to complete the listed elementary symmetric polynomials with a new one.
. From this definition, you can
try to complete the listed elementary symmetric polynomials with a new one.

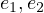 and
and 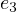 . It is often useful to represent symmetric equations using
elementary symmetric polynomials (more about this later).
. It is often useful to represent symmetric equations using
elementary symmetric polynomials (more about this later).
Something that holds a specific point of interest is the expressions of the form
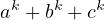 . For this specific problem there exists the Newton-Girard Formula for
Symmetric Polynomials. Define a function
. For this specific problem there exists the Newton-Girard Formula for
Symmetric Polynomials. Define a function 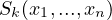 in the following way.
in the following way.
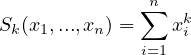
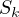 .
.
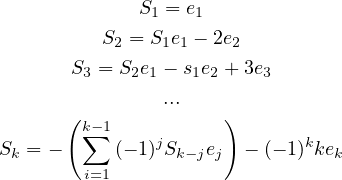
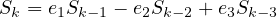
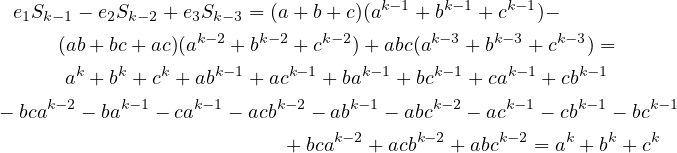 |
Consider a simple inequality.
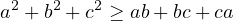
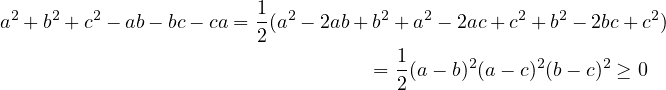 |
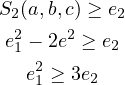
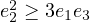 . We can prove this
by just substituting the definitions of
. We can prove this
by just substituting the definitions of 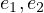 and
and 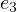 .
. 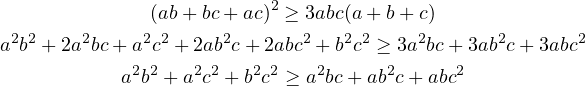
![x = [ab,bc,ac]](symmetric_polynomials25x.png) and the same
and the same ![y = [ab,bc,ac]](symmetric_polynomials26x.png) , we assume
, we assume 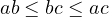 and get
the following.
and get
the following. 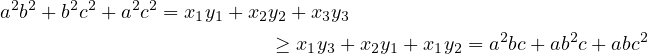 |
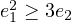 and
and 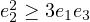 ) are the most useful ones. Using
these inequalities along with basic usage of other common inequalities can
help solve a variety of different problems. One might notice that most of
the techniques somehow transform an equation or inequality into a form
involving purely elementary symmetric polynomials and can ask the question:
what if such a form does not exist? Happily, for us, there is a theorem called
the Fundamental Theorem of Symmetric Polynomials, which claims that
any symmetric polynomial can, in fact, be expressed as an expression using
elementary symmetric polynomials (the theorem applies to any number of
variables). The proof of this statement will also not be provided here due to its
complexity.
) are the most useful ones. Using
these inequalities along with basic usage of other common inequalities can
help solve a variety of different problems. One might notice that most of
the techniques somehow transform an equation or inequality into a form
involving purely elementary symmetric polynomials and can ask the question:
what if such a form does not exist? Happily, for us, there is a theorem called
the Fundamental Theorem of Symmetric Polynomials, which claims that
any symmetric polynomial can, in fact, be expressed as an expression using
elementary symmetric polynomials (the theorem applies to any number of
variables). The proof of this statement will also not be provided here due to its
complexity.
Say we have three systems of symmetric equations as the following.
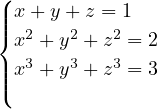
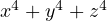 , for example. First of all, transform the
equations using elementary symmetric polynomials.
, for example. First of all, transform the
equations using elementary symmetric polynomials. 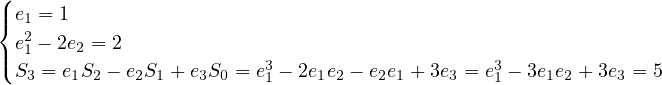
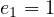 ,
, 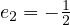 and from the third equation we can find
and from the third equation we can find
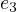 .
. 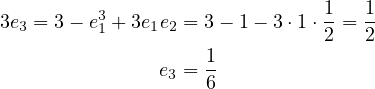
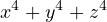 using the
Newton-Girard Formula.
using the
Newton-Girard Formula. 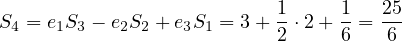
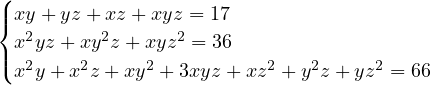
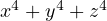 . Do the same as last time: express the system using
elementary symmetric polynomials.
. Do the same as last time: express the system using
elementary symmetric polynomials. 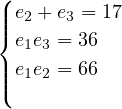
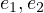 and
and 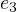 .
. 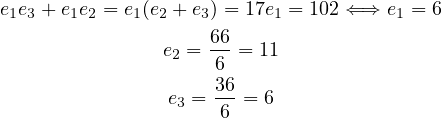
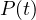 such that
such that 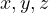 are all roots of that polynomial. This
would be useful as from there we can immediately find the solution in the following
way.
are all roots of that polynomial. This
would be useful as from there we can immediately find the solution in the following
way. 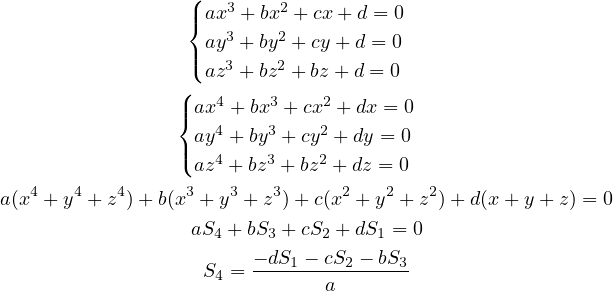
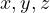 to be roots of a
polynomial
to be roots of a
polynomial 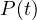 , simply let
, simply let 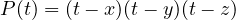 . Expanding out the
expression, we get the following.
. Expanding out the
expression, we get the following. 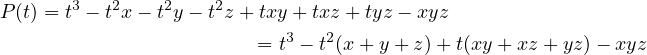 |
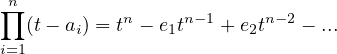
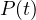 .
. 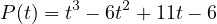
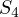 is to calculate
is to calculate 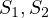 and
and
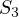 .
. 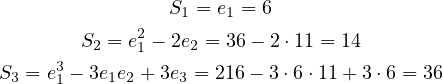
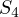 .
. 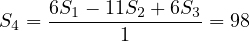
 is unnecessary; one could replace all the calculations
by simply calculating
is unnecessary; one could replace all the calculations
by simply calculating 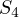 through
through 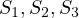 and
and 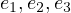 . In fact, what was
just described is yet another proof or perspective on the Newton-Girard
Formula. Obviously, in such cases, using the Newton-Girard Formula directly
is best. However, if you forgot, you could always remember it using this
trick.
. In fact, what was
just described is yet another proof or perspective on the Newton-Girard
Formula. Obviously, in such cases, using the Newton-Girard Formula directly
is best. However, if you forgot, you could always remember it using this
trick.