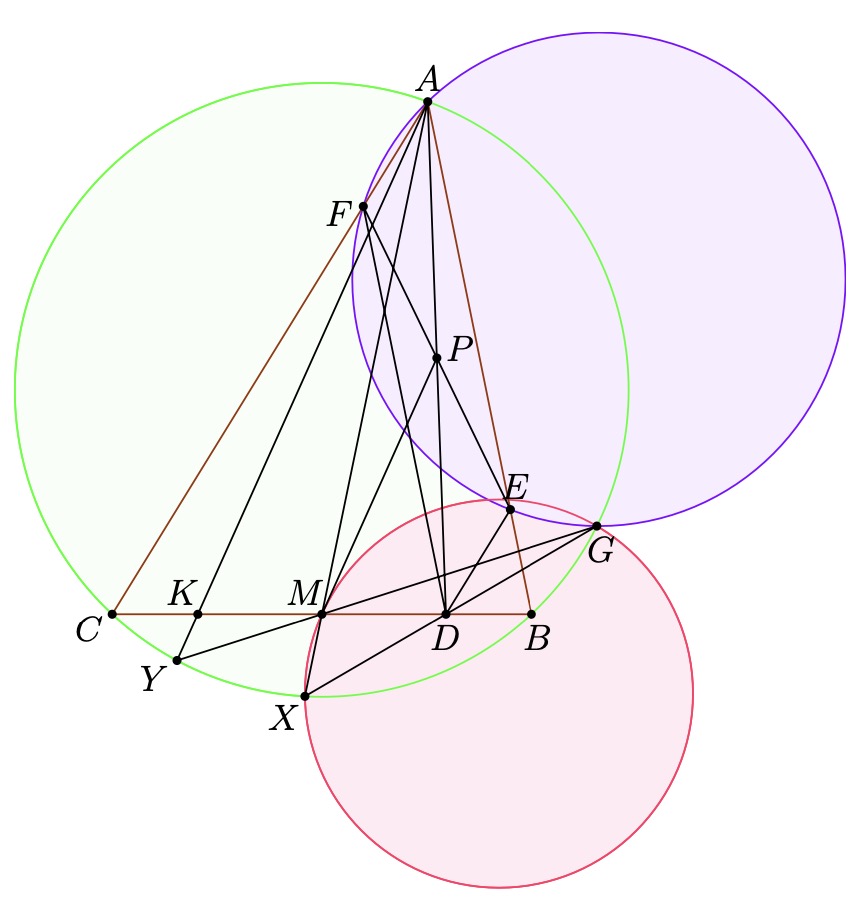
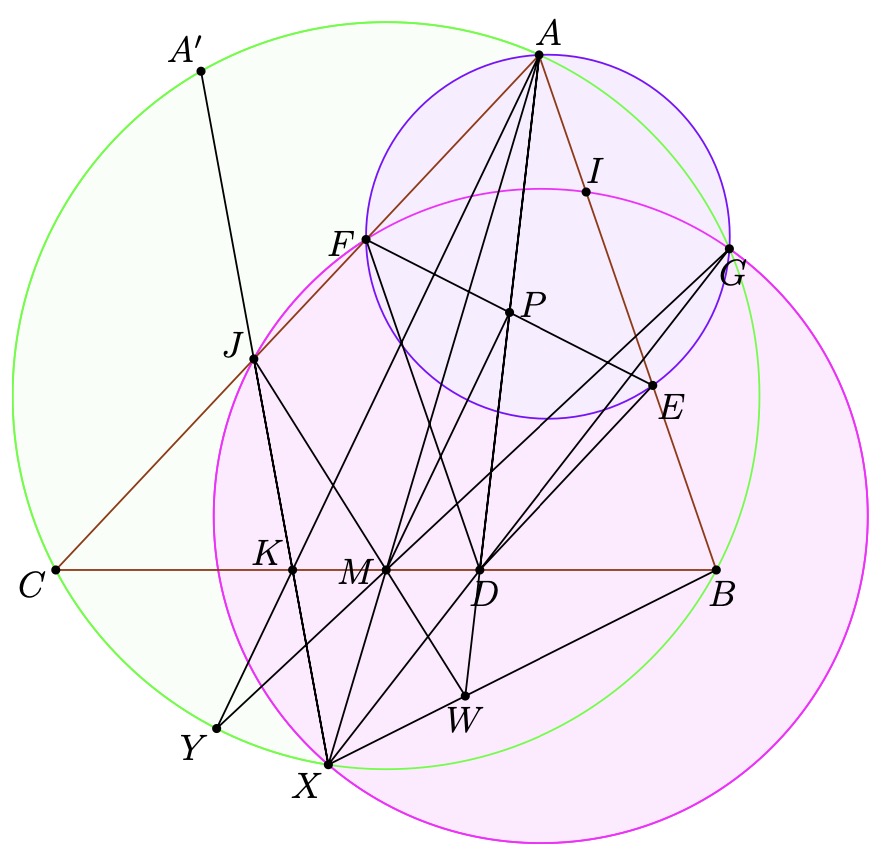
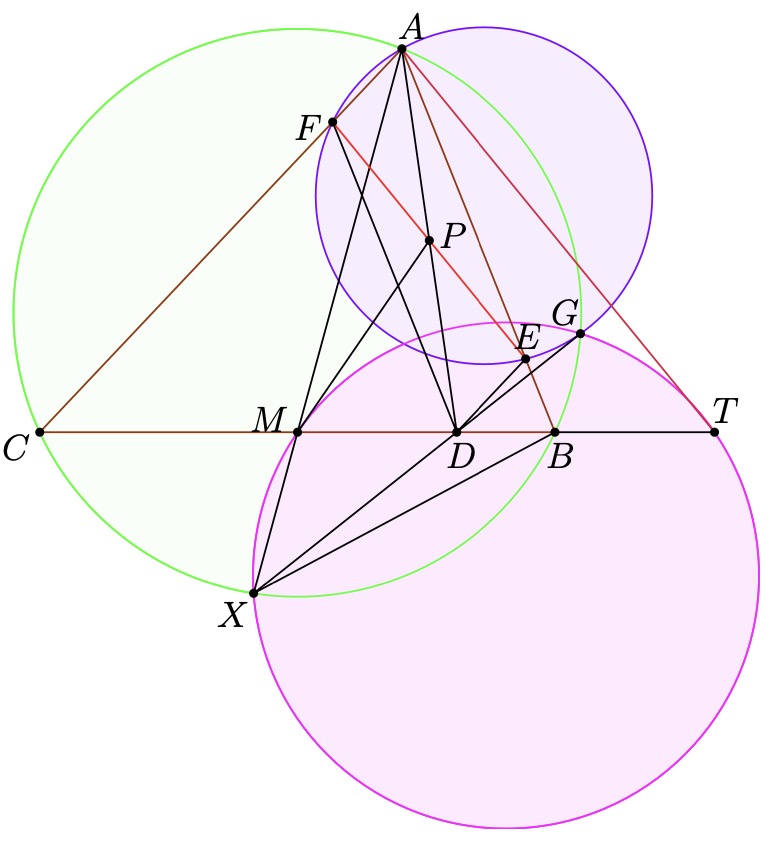
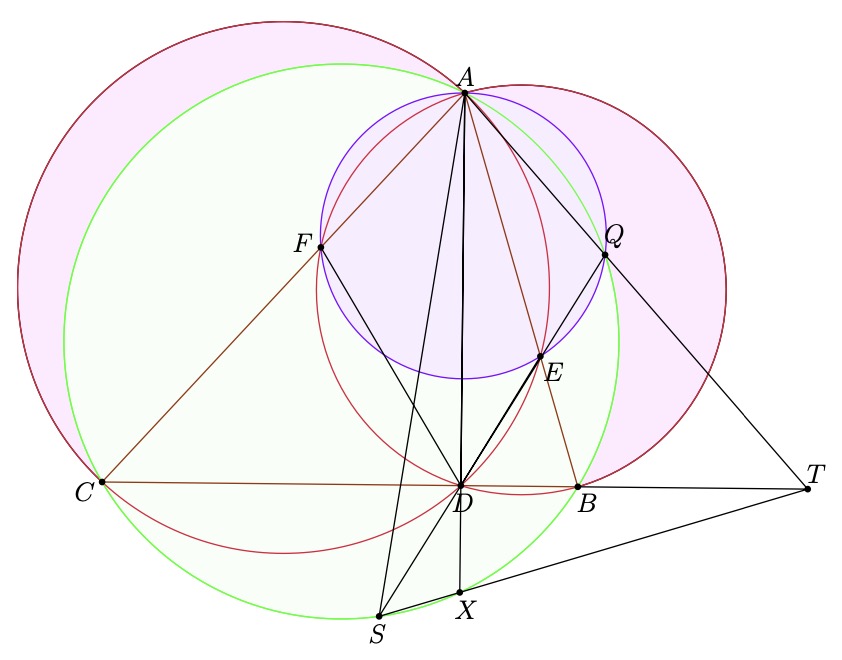
Problem 1 (AoPS). Given a triangle 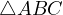 , let
, let 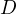 be an arbitrary point
on
be an arbitrary point
on 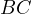 , then let
, then let 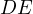 and
and 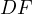 be parallel to
be parallel to 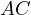 and
and 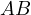 respectively.
Let
respectively.
Let 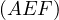 intersect
intersect 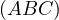 at
at 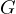 , let
, let 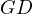 intersect
intersect 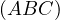 at
at 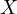 .
Prove, that if
.
Prove, that if 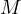 is the midpoint of
is the midpoint of 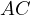 , then
, then 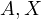 and
and 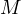 are colinear.
are colinear.
Problem 1 (AoPS). Given a triangle 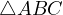 , let
, let 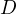 be an arbitrary point
on
be an arbitrary point
on 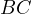 , then let
, then let 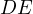 and
and 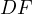 be parallel to
be parallel to 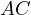 and
and 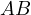 respectively.
Let
respectively.
Let 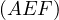 intersect
intersect 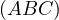 at
at  , let
, let  intersect
intersect 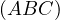 at
at 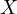 .
Prove, that if
.
Prove, that if 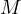 is the midpoint of
is the midpoint of 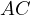 , then
, then 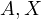 and
and 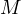 are colinear.
are colinear.
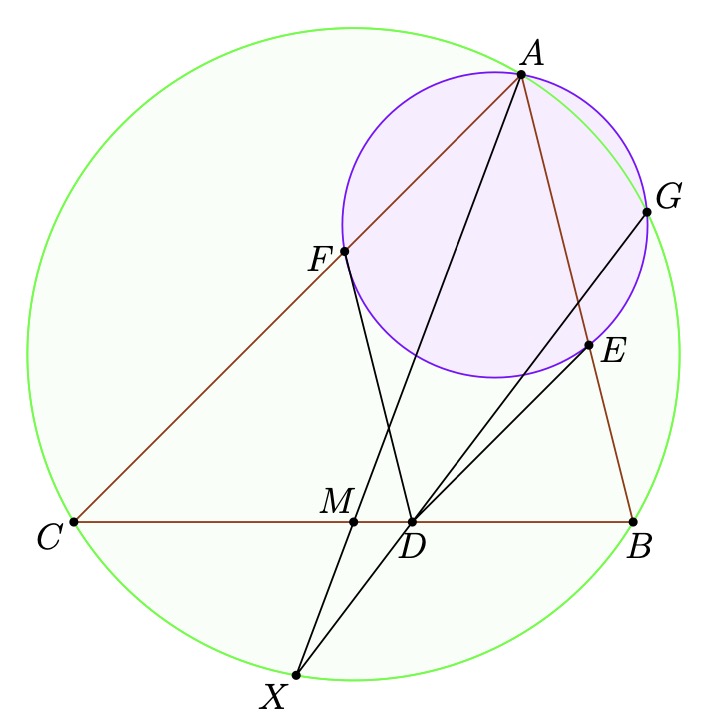
This theorem can be proven in various ways, the first way and arguably most beautiful way is using the Butterfly theorem, (thanks @KrazyNumberMan)
Proof. Let  be the intersection of
be the intersection of 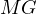 with
with 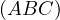 and let
and let 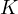 be the
intersection of
be the
intersection of 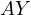 with
with 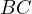 and
and 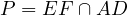 . Then,
. Then,
indeed, since 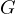 is the Miquel point of
is the Miquel point of 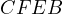 it must be that
it must be that
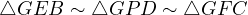 , consequently,
, consequently,
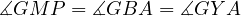
thus implying the desired result. 
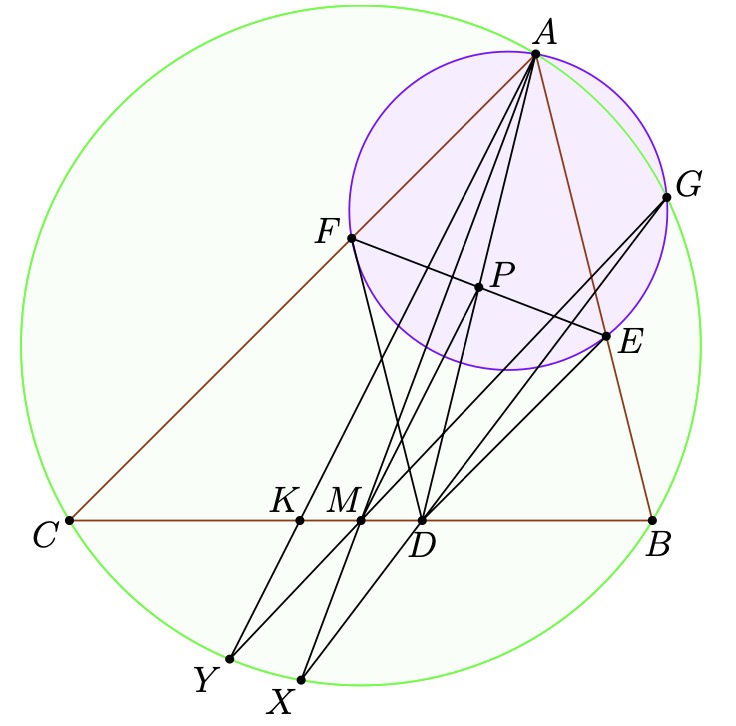
Since 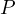 is the midpoint of
is the midpoint of 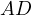 and
and 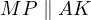 it must be that
it must be that 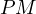 is the
midline in
is the
midline in 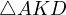 , thus
, thus 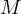 is the midpoint of
is the midpoint of 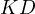 . Thus, by the Butterfly
theorem it must be that
. Thus, by the Butterfly
theorem it must be that 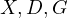 are colinear. __
are colinear. __
Another proof of the original theorem involves constructing the symmedian, the proof in itself is not particularly interesting, however the results shown are somewhat reasonable.
Proof. Let us prove that,
Using coaxility lemma, all we have to prove is that,
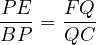
Then this would mean that 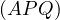 passes through
passes through 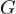 , where we define
, where we define 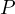 and
and 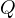 to be the intersection points of
to be the intersection points of 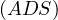 with
with 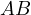 and
and 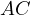 . Notice,
. Notice,
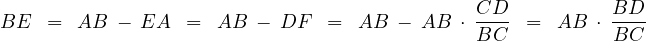 |
Now let us try calculating the value of 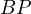 , this can be done through the Power
of the Point,
, this can be done through the Power
of the Point,
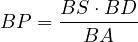 |
Thus,
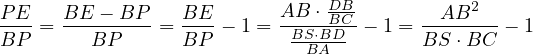 |
We want to show this is the same as,
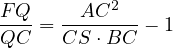 |
(same logic for this expression). Let us use the formula for the length of 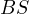 (because the symmedian is the isogonal conjugate of the median),
(because the symmedian is the isogonal conjugate of the median),
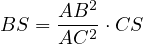
Thus,
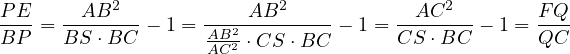 |
This finishes the proof of the lemma, thus 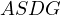 is cyclic.
is cyclic. 
It is quite well known that if 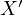 is the intersection of
is the intersection of 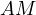 with
with  ,
then
,
then 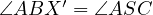 .
.
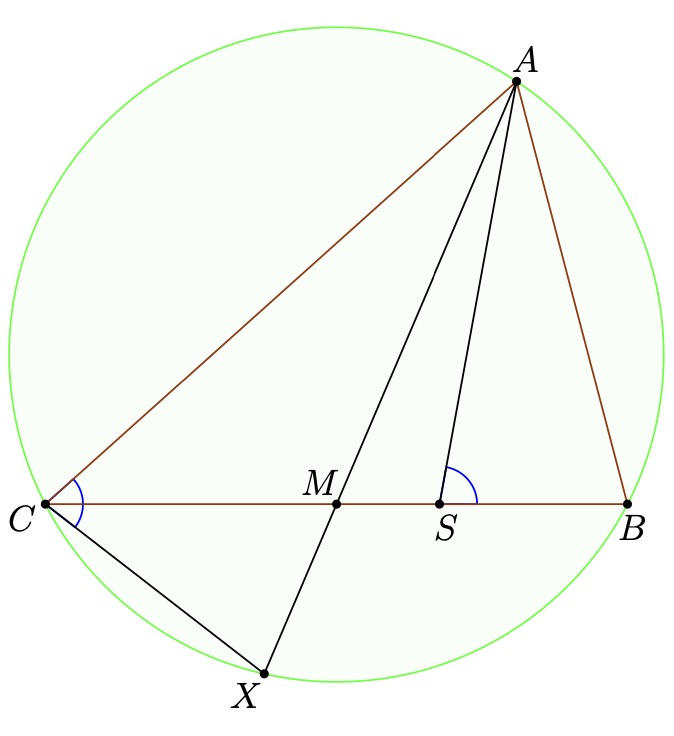
this is just obvious because 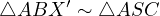 , due to
, due to 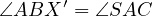 and
and
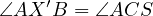 .
. 
Now going back to our problem, notice that,
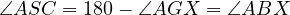
Because only one point satisfies such condition it must mean that 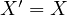 in
other words,
in
other words, 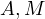 and
and 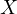 are colinear.
__
are colinear.
__
Now, given this powerful configuration let extend it and consider some other problems,
Proof. Notice,
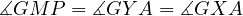
which proves the desired tangency. __
Proof. (thanks @keglesnit)
Let 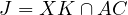 and let
and let 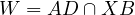 , then let us prove that
, then let us prove that 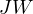 passes through
passes through 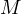 . Let
. Let 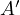 be the second intersection of
be the second intersection of 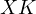 with
with 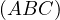 .
Then,
.
Then,
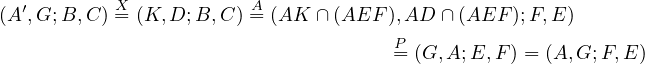 |
Note 1. The fact that 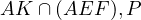 and
and 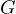 lie on one line directly
follows from angle chase similar to that done in the proof of the Anchor Point
Lemma
lie on one line directly
follows from angle chase similar to that done in the proof of the Anchor Point
Lemma
This implies that 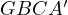 is similar to
is similar to 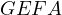 . Thus,
. Thus,
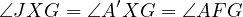
consequently it must be that 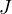 is the intersection of
is the intersection of 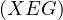 with
with
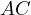 .
.
Now, all that is left to show that 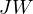 passes through
passes through 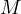 .
.
Let 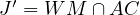 , then by Desargues Involution Theorem (DIT)
applied to
, then by Desargues Involution Theorem (DIT)
applied to 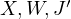 and
and 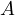 , there exists an involution swapping
, there exists an involution swapping
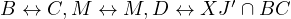 . Consequently the involution must be a reflection
over
. Consequently the involution must be a reflection
over 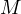 , thus
, thus 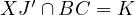 , thus
, thus 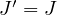 .
.
Consequently it must be that 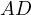 ,
,  and
and 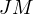 are concurrent. __
are concurrent. __
Proof. Notice,  , consequently projecting from
, consequently projecting from  we
obtain,
we
obtain,
where 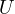 is the intersection of a line parallel to
is the intersection of a line parallel to 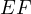 through
through 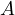 with
with
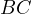 . However, since
. However, since 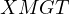 is cyclic it must be that
is cyclic it must be that 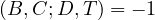 .
(since
.
(since 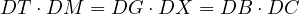 ) Consequently
) Consequently 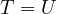 , thus
, thus 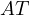 is parallel to
is parallel to 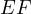 . __
. __
While the original statement is useful, it can rarely be used in problem due to a rather peculiar condition on parallel lines. Thankfully there exists a far more useful generalized of the theorem,
Problem 5 (Generalized Anchor Point Lemma). Let 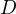 be an arbitrary
point on
be an arbitrary
point on 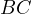 in
in 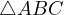 . Let there be two fixed directions
. Let there be two fixed directions 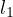 and
and 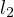 .
Let
.
Let 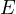 and
and 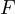 be the intersection of two lines through
be the intersection of two lines through 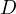 parallel to
parallel to 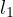 and
and 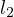 with
with 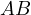 and
and 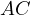 . Let
. Let 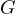 be the intersection of
be the intersection of 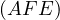 and
and
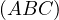 . Prove that
. Prove that 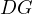 passes through a constant point on
passes through a constant point on 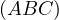 .
.
Also prove that the circles 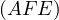 are all coaxial and the second constant
point is the intersection of the circle with the line isogonal to
are all coaxial and the second constant
point is the intersection of the circle with the line isogonal to 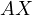 in
in 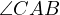 with
with 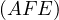 .
.
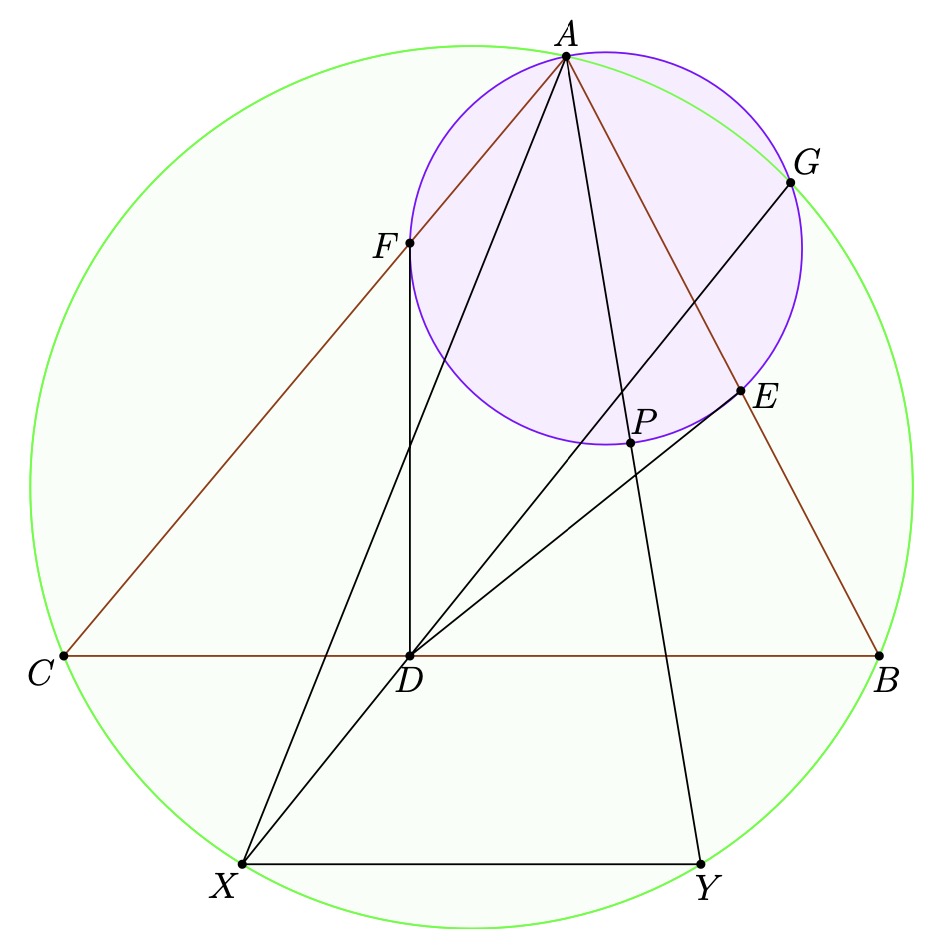
Proof. Maybe it is possible to extend the synthetic approach described earlier,
however it is far more simpler to use the Cool Ratio Lemma. Let 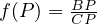 ,
then,
,
then,
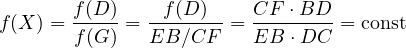
thus since 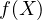 is constant it must be that
is constant it must be that 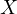 is constant. __
is constant. __
Now I will outline a technique which is sometimes very powerful in simplifying a
problem which involves some intersection of some circle with 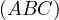 . Let us go
through some well known configurations and attack them with the Generalized
Anchor Point Lemma.
. Let us go
through some well known configurations and attack them with the Generalized
Anchor Point Lemma.
Problem 6 (Sharky-Devil Configuration). Let
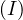 be the incircle of
be the incircle of 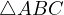 , let
, let 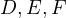 be the tangency points of
be the tangency points of 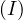 with
with 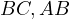 and
and 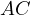 , respectively. Let
, respectively. Let 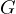 be the second intersection of
be the second intersection of
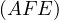 with
with 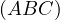 . Let
. Let 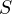 be the midpoint of the arc
be the midpoint of the arc 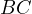 . Prove that
. Prove that
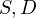 and
and 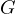 are colinear.
are colinear.
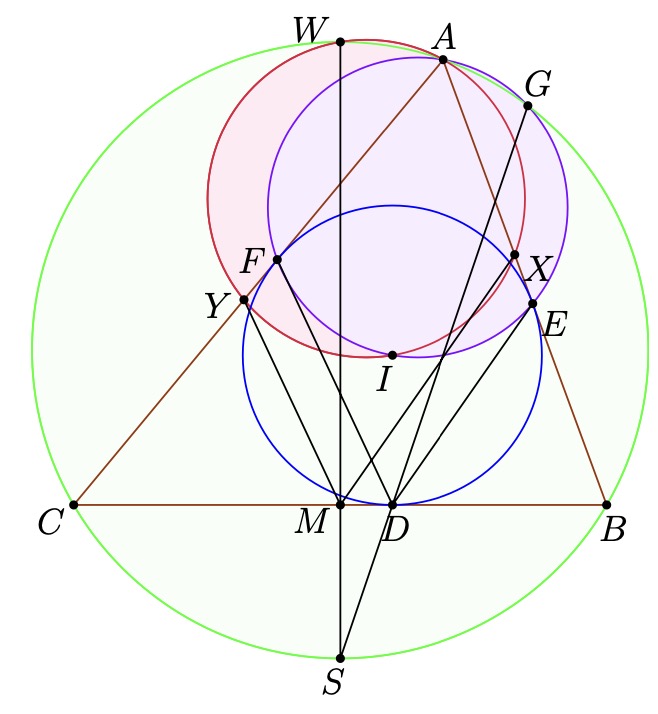
Proof. Let us introduce  the midpoint of
the midpoint of 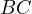 and
and 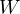 the midpoint of
the larger arc
the midpoint of
the larger arc 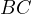 . Then, let
. Then, let 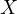 and
and 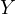 be the intersections of the lines
through
be the intersections of the lines
through 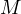 parallel to
parallel to 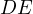 and
and 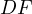 with
with 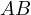 and
and 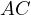 , respectively.
By the Generalized Anchor Point Lemma all that is left to prove is that
, respectively.
By the Generalized Anchor Point Lemma all that is left to prove is that
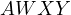 is cyclic.
is cyclic.
Notice, since,
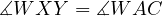
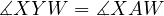
which implies that 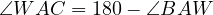 , however this is only true for
, however this is only true for
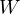 being the midpoint of the larger arrc
being the midpoint of the larger arrc 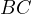 . Thus
. Thus 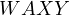 is cyclic
which proves one of the properties of the Sharky-Devil point. (Amusingly
is cyclic
which proves one of the properties of the Sharky-Devil point. (Amusingly 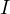 lies on this circle as well due to
lies on this circle as well due to 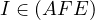 and
and 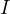 lying on the angle bisector
of
lying on the angle bisector
of  ). __
). __
Problem 7 (USA TST 2012 P1). In acute triangle ABC, ∠A < ∠B and ∠A < ∠C. Let P be a variable point on side BC. Points D and E lie on sides AB and AC, respectively, such that BP = PD and CP = PE. Prove that as P moves along side BC, the circumcircle of triangle ADE passes through a fixed point other than A.
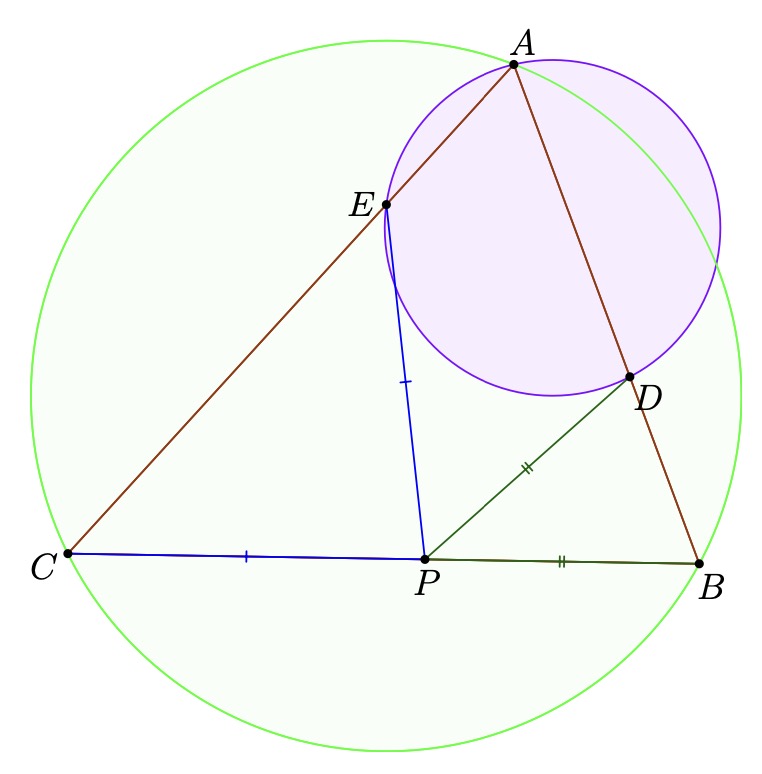
Proof. Since as we move  the lines
the lines  and
and 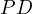 are parallel to two
fixed directions, thus by the Generalized Anchor Point Lemma it must be that
are parallel to two
fixed directions, thus by the Generalized Anchor Point Lemma it must be that
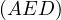 passes through a fixed point. __
passes through a fixed point. __
Problem 8 (ELMO 2013 Shortlist G3). n △ABC, a point D lies on line BC. The circumcircle of ABD meets AC at F (other than A), and the circumcircle of ADC meets AB at E (other than A). Prove that as D varies, the circumcircle of AEF always passes through a fixed point other than A, and that this point lies on the median from A to BC.
Proof. Notice, 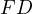 and
and 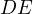 point in constant directions, since
point in constant directions, since
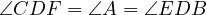 . Thus, by the Generalized Anchor Point Lemma all we
need to do is show for one position of
. Thus, by the Generalized Anchor Point Lemma all we
need to do is show for one position of 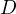 that
that 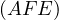 passes through some
fixed point on the median. Let us fix
passes through some
fixed point on the median. Let us fix 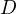 to be the foot of the altitude
from
to be the foot of the altitude
from 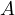 to
to 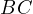 . Let
. Let 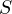 be the intersection of the symmedian from
be the intersection of the symmedian from
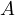 with
with 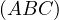 , then, (it is well known, however the proof is outlined
below)
, then, (it is well known, however the proof is outlined
below)
indeed, since 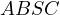 is harmonic, by projecting from
is harmonic, by projecting from 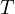 it must be that
it must be that
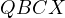 is harmonic, consequently projecting from
is harmonic, consequently projecting from 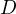 we obtain that
we obtain that 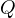 goes to
a point
goes to
a point 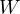 on
on 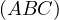 such that
such that 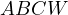 is harmonic, thus
is harmonic, thus 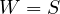 , thus
, thus
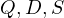 are colinear.
are colinear. 
Now, by the Generalized Anchor Point Lemma since 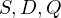 are colinear, it
must be that
are colinear, it
must be that 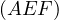 passes through a fixed point lying on the isogonal line to
passes through a fixed point lying on the isogonal line to
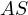 in
in 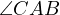 which is the median. __
which is the median. __
The problem with the Anchor Point Lemma and its generalization that it assumes
that the lines stay parallel with respect to each other. The motivation for this
generalization is that this can be interpreted as a pencil of lines through some
point at infinity, so what happens if we move that point into 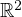 ? It turns
out not any two pairs of points will keep the theorem true, however each
point given a point on
? It turns
out not any two pairs of points will keep the theorem true, however each
point given a point on 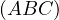 has precicely one conjugate (which will be
referenced as the Anchor Point Conjugate further on) which preserves this
theorem.
has precicely one conjugate (which will be
referenced as the Anchor Point Conjugate further on) which preserves this
theorem.
Problem 9 (AoPS). Let 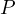 be an arbitrary fixed point and
be an arbitrary fixed point and 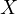 an abitrary
fixed point on
an abitrary
fixed point on 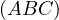 . Let
. Let 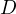 be an abritrary point on
be an abritrary point on 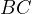 . Let
. Let 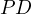 intersect
intersect 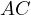 at
at 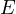 . Let
. Let  intersect
intersect 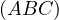 at
at 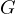 . Let
. Let 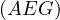 intersect
intersect 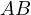 a second time at
a second time at  . Prove that the line
. Prove that the line  passes through a
constant point
passes through a
constant point 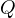 as
as 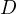 moves on
moves on 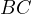 , and that
, and that 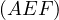 passes through
a fixed point
passes through
a fixed point 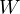 .
.
This theorem can trivially be proved via moving points, unfortunately, I do not possess any synthetic solution.
The Generalized Anchor Point Lemma is simply a special case of the
Advanced Anchor Point Lemma where  lies on the line at infinity, then it
simply claims that the Anchor Point Conjugate lies on the line at infinity as
well.
lies on the line at infinity, then it
simply claims that the Anchor Point Conjugate lies on the line at infinity as
well.
Interestingly,
Proof. The map can be constructed like this, let  be on BC such that
be on BC such that
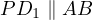 and let
and let 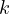 be the line through
be the line through 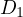 parallel to
parallel to 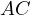 . Let
. Let 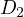 be on BC so
be on BC so 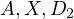 are colinear.
are colinear.
Then if 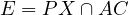 and
and 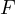 is such that
is such that 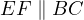 . Then,
. Then,
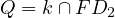 .
.
Consequently it must be that if 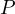 moves projectively,
moves projectively, 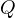 moves
projectively as well. __
moves
projectively as well. __
I believe that the Generalized Anchor Point Method is quite powerful in problems
invovling some type of intersection of 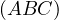 with a circle passing through
with a circle passing through 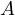 with well defined intersections with
with well defined intersections with 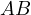 and
and 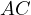 .
.
Note 2 (TODO). Additional problems that can be solved using this method will be added to this document as I come across them.