Theorem 1. Consider the chord 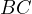 in the circle
in the circle 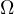 . Let the circle
. Let the circle 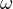 touch
touch 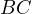 at a point
at a point 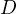 and the circle
and the circle 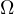 at a point
at a point 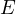 . Prove that the
line
. Prove that the
line 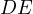 passes through
passes through 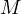 , the middle of the larger arc
, the middle of the larger arc 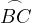 .
.
This paper compiles a collection of geometric proofs and related constructions that center around Sawayama’s Lemma and Thebault’s theorem. The document begins with the presentation and proof of the Shooting Lemma, which establishes a relationship between a chord in a circle, a tangent circle, and the midpoint of the larger arc. Using this foundational lemma, the proofs of Sawayama’s Lemma and Verrier’s Lemma follow, demonstrating the collinearity of specific points associated with inscribed triangles and tangent circles. The final section extends these results to prove Thebault’s theorem, generalizing the principles of Sawayama’s and Verrier’s Lemmas to a broader context involving two tangent circles.
Theorem 1. Consider the chord 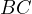 in the circle
in the circle 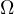 . Let the circle
. Let the circle 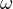 touch
touch 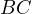 at a point
at a point 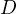 and the circle
and the circle 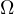 at a point
at a point 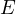 . Prove that the
line
. Prove that the
line 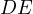 passes through
passes through 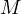 , the middle of the larger arc
, the middle of the larger arc 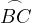 .
.
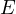 , which transforms
, which transforms 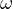 into
into 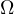 . Then,
. Then, 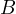 is mapped to
is mapped to 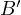 and
and 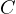 to
to
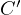 , where
, where 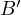 and
and 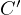 are the intersections of
are the intersections of 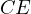 and
and 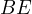 with the
tangent from
with the
tangent from 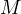 to
to 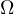 respectevely.
respectevely.
Then, 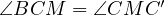 due to
due to 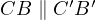 , and
, and 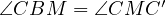 because
because
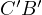 touches
touches 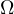 and finally
and finally 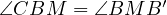 . Thus,
. Thus, 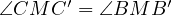 ,
however due to
,
however due to 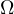 touching
touching 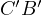 we know that
we know that 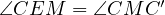 and
and
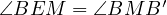 , consequently
, consequently 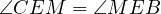 . In other words
. In other words 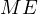 is
the bisector of
is
the bisector of 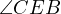 which means that
which means that 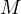 is the middle of the larger arc
is the middle of the larger arc
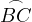 .
.
In fact, due to 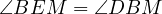 we conclude that
we conclude that 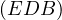 touches
touches 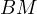 ,
consequently,
,
consequently,
| (1) |
And due to 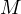 being the middle of
being the middle of 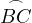 it must be that
it must be that 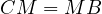 , thus,
, thus,
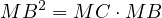 . Combining these results we get a nice formula,
. Combining these results we get a nice formula,
| (2) |
The figure can also show a lot of interesting and fundemental properties if one
performs an inversion centered at the point 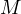 with a radius of
with a radius of 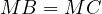 .
Then through this process
.
Then through this process 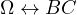 and because
and because 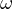 must continue to touch
must continue to touch
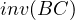 and
and 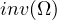 (in other words
(in other words 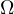 and
and 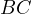 ) and it must be in the same
angle from
) and it must be in the same
angle from 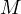 , it must be the case that
, it must be the case that 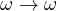 under the inversion.
Consequently, it must mean that
under the inversion.
Consequently, it must mean that 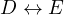 and thus
and thus 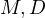 and
and 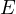 are colinear.
Another consequence of such argument is that the length of the tangents from
are colinear.
Another consequence of such argument is that the length of the tangents from 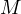 to
to 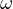 are equal to
are equal to 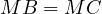 .
.
Now let us consider the following, a bit stronger statement,
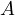
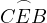
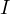
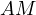
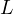
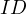
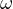
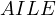
This is also quite a trivial statement, noticing from the previous statement
that 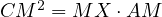 and
and 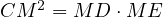 we can conclude that
we can conclude that
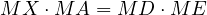 which by the power of the point
which by the power of the point 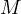 concludes that
concludes that
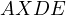 is cyclic. Now, all that is left to notice is that,
is cyclic. Now, all that is left to notice is that, 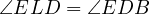 due to
due to 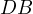 touching
touching 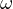 and
and 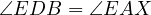 due to
due to 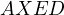 being
cyclic, thus
being
cyclic, thus 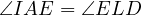 and
and 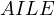 is cyclic.
is cyclic.
It is a bit interesting to see the behaviour of 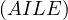 as one moves
as one moves
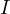 along
along 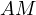 . When
. When 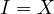 we get an already proven statement that
we get an already proven statement that
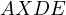 is cyclic and when
is cyclic and when 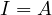 we see that
we see that 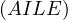 touches
touches 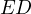 .
However, there is a more important position of
.
However, there is a more important position of 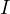 which has the following
property.
which has the following
property.
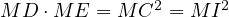 , thus
, thus 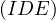 touches
touches 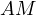 . Consequently,
. Consequently,
| (3) |
due to 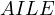 being cyclic. Which implies that
being cyclic. Which implies that 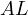 touches
touches 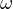 .
.
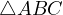
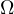
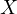
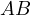
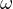
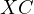

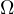
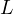
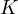
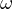
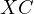

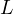
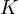
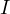
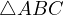
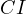 till the intersection with
till the intersection with 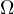 , let that
intersection point be
, let that
intersection point be 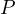 . Then, due to the Trillium theorem it is clear
that
. Then, due to the Trillium theorem it is clear
that 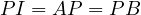 . This allows one to apply the last lemma to this
configuration. Here
. This allows one to apply the last lemma to this
configuration. Here 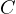 is serves as the arbitrary point from the last lemma and
due to
is serves as the arbitrary point from the last lemma and
due to 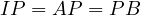 it must be that the intersection of
it must be that the intersection of 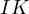 with
with 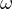 ,
let that point be
,
let that point be 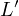 , must be the tangency point from
, must be the tangency point from 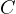 to
to 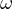 .
.
However, that tangency point is 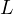 by definition, thus
by definition, thus 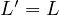 and
consequently
and
consequently 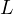 ,
, 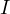 and
and 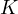 are colinear.
are colinear.
Now consider what happens when one moves 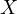 along
along 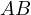 , specifically
let
, specifically
let 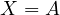 . Then, Sawayama’s lemma will transform itself into Verrier’s
lemma.
. Then, Sawayama’s lemma will transform itself into Verrier’s
lemma.
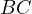
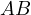
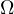
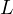
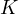
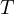
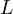
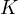
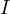
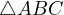
This statement has other proofs which do not involve Sawayama’s lemma, one of the most notable ones is the following which showcases the mechanism at play.
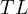 and
and 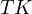 with
with 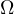 in points
in points 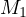 and
and 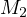 ,
by the shooting lemma it must be that
,
by the shooting lemma it must be that 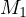 and
and 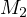 are the middle’s of arcs
are the middle’s of arcs
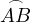 and
and 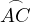 . Consequently they must lie on the lines
. Consequently they must lie on the lines 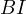 and
and 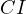 .
.
All that is left is to apply Pascal’s theorem for 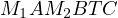 and conclude that
and conclude that
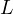 ,
, 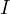 and
and 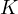 are colinear.
are colinear.
A beautiful lemma about the 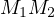 is the following,
is the following,
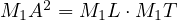 and
and 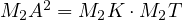 . This, means
that,
. This, means
that,
| (4) |
| (5) |
Thus, it must be that 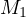 and
and 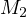 lie on the radical axis of
lie on the radical axis of 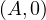 and
and  , in
other words
, in
other words 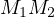 is the radical axis of
is the radical axis of 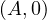 and
and  .
.
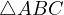
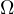
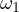

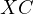
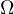
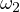
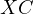
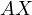
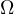
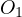
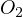
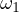
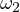
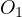
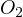
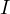
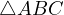
Notice, due to Sawayama’s lemma it must be that 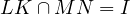 , where
, where
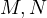 are the tangency points of
are the tangency points of 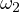 with
with 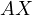 and
and 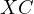 and
and 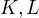 are
the tangency points of
are
the tangency points of 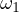 with
with  and
and 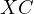 . With this in mind I suggest
looking at the problem from another perspective,
. With this in mind I suggest
looking at the problem from another perspective, 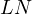 is the inner tangent
between
is the inner tangent
between 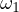 and
and 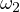 and
and 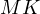 is the outer tangent between
is the outer tangent between 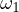 and
and 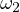 .
One must prove that
.
One must prove that 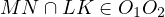 .
.
As it turns out this statement is true for arbitrary circles 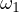 and
and 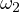 .
.
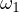
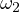
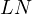
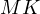
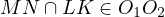
This is a wonderful statement to consider on its own. Proving this statement
automatically proves Thebault’s theorem. Let us consider the homothepy center 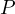 which transforms
which transforms 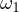 to
to 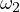 (in other words the intersection of the two outer
common tangents). Let
(in other words the intersection of the two outer
common tangents). Let 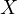 and
and 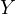 be the points of tangency of the common
tangent of
be the points of tangency of the common
tangent of 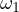 and
and 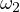 . Let
. Let 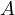 and
and 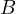 be the intersection of
be the intersection of 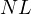 with
with 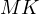 and
and 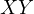 respectively. Consider the triangle
respectively. Consider the triangle 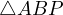 , then
, then
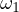 is its incircle and
is its incircle and 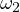 is its excircle. Then, by the Iran lemma the
projection of
is its excircle. Then, by the Iran lemma the
projection of 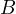 onto the bisector of
onto the bisector of 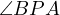 must lie on both
must lie on both 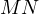 and
and
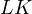 .
.
In other words, the projection of 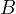 onto the bisector of
onto the bisector of 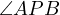 is
is
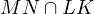 . However, the projection of
. However, the projection of 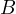 onto the bisector of
onto the bisector of 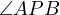 obviously is part of
obviously is part of 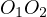 . Thus,
. Thus, 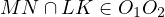 and the lemma is proven,
proving Thebault’s theorem.
and the lemma is proven,
proving Thebault’s theorem.